Bu tip dinamik bir analiz için türev mantığıyla gitmek lazım, yani marjinal getiri ile marjinal eurobond fiyat değişimi (artı marjinal kazanılan ek faiz) düşünmek lazım. Fazla detaya inmeden bakalım:
Turkey 2030 %11.875 $ Eurobond (piyasada kupon faizi Amerikan geleneğine göre 11 7/8 olarak ifade edilir)
2013 yılında piyasa faizi %4 ise yaklaşık durasyon: 10 yıl, yani her %1'lik faiz değişimi, fiyatı %10 etkiliyor.
4 yıl içinde Eurobond faizi 2 puan artacaksa; fiyatı da %20 düşecek demektir. Ayrıca, 4 yıl içerisinde mevduata kıyasla 1 x 4 = 4 puan ekstra faiz getiri verecek (mevduat faizinin bu 4 yılda lineer biçimde arttığını varsaydım, bu nedenle dönemsel ortalama faizi %3 olacaktır. Eurobondu alan kişi 4 faize razı olduğundan hep bununla olan farka bakılmalı) ... Sonuçta 20 > 4 olduğundan 2013'te bu uzun vadeli Eurobondu almak yerine mevduat yapmak veya çok daha kısa vadeli bir Eurobond seçmek daha doğru olacaktır.
(not: 2013'te elinde TL olan biri bunu hesaplıyorsa, 2013-2017 arasındaki kur farkını hesaba katması gerekir ki o zaman işler çok değişir. Biz hep dolar mevduatta olan biri için baktık).
2017'den ileri baktığımızda ise, şu anki durasyon 7.8 yıla indi deyip, benzeri hesabı sizlere bırakıyorum.
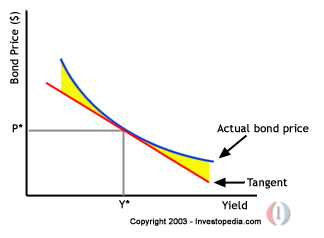
Dip not: durasyon, sadece kısa vadeli piyasa hareketlerinin etkisini çok yakın olarak verir -approximation-. 4 yıl ise uzun bir süre, tahvilin fiyat-faiz eğrisinde bulunulan noktanın tanjantının zaman içinde sürekli eğim değiştirmesi sebebiyle (diğer adıyla konveksite), doğru bir hesap ancak detaya girerek bulunur. Biz biraz daha defter arkası hesabıyla bakıyoruz bu aşamada. Yine görselleştirirsek daha net ortaya çıkar. Grafikte biz tanjantın üzerinde kayıyoruz ve gittiğimiz yeri "fiyat" olarak hesaplıyoruz. Ancak sarı kısım bizim hata payımız çünkü bu bir eğri ve doğrusal gitmiyor; yani ne kadar uzağa gidersek tanjant o kadar hata payı içeriyor; uzaklaştıkça hesabı verileri güncelleyerek "yeni tanjant çizerek" yapmak gerekir:












Yer İmleri